Hola a todos mi nombre es Gustavo Adolfo Salas Coronado de la clase de los jueves de v1 a v3 y este es mi proyecto y explicare cada uno de los puntos requeridos:
1- Problema que este algoritmo resuelve.
El algoritmo de Floyd-Warshall, descrito en 1959 por Bernard Roy, es un algoritmo de análisis sobre grafos para encontrar el camino minimo en grafos dirigidos ponderados. El algoritmo encuentra el camino entre todos los pares de vértices en una única ejecución. El algoritmo de Floyd-Warshall es un ejemplo de programacion dinamica.
2.- Definicion formal.
Pues el algoritmo de Floyd-Warshall compara todos los posibles caminos a través del grafo entre cada par de vértices. El algoritmo es capaz de hacer esto con sólo V3 comparaciones (esto es notable considerando que puede haber hasta V2 aristas en el grafo, y que cada combinación de aristas se prueba). Lo hace mejorando paulatinamente una estimación del camino más corto entre dos vértices, hasta que se sabe que la estimación es óptima, por lo tanto es un algoritmo de OPTIMIZACION.
3.-La complejidad computacional de este algoritmo es de tipo P determinista ya que puede ser resuelto por una maquina turing determinista en tiempo polinomico.
4.-Pseudocodigo.
Inicializar
D = A ' matriz de distancias = matriz de arcos
si i=j o Dij= infinito entonces Pi,j = nulo sino Pi,j=i 'matriz de caminos
for k = 1 to V
for i = 1 to V
for j = 1 to V
Di,j = min(Di,j , Di,k + Dk,j )
si min = Di,k + Dk,j entonces
Pi,j = Pk,j
fin
Si utilizamos matrices booleanas, para encontrar todos los n2 de
5.- Analisis asintotico.
 desde
desde  se necesita hacer 2n2 operaciones binarias. Debido a que empezamos con
se necesita hacer 2n2 operaciones binarias. Debido a que empezamos con  y computamos la secuencia de n matrices booleanas
y computamos la secuencia de n matrices booleanas  ,
, 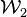 , ...,
, ...,  , el número total de operaciones binarias es de
, el número total de operaciones binarias es de 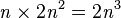 . Por lo tanto, la complejidad del algoritmo es Θ(n3) y puede ser resuelto por una maquina determinista de turing en tiempo polinomico.
. Por lo tanto, la complejidad del algoritmo es Θ(n3) y puede ser resuelto por una maquina determinista de turing en tiempo polinomico.6.- EJEMPLO.
Hallar el camino mínimo desde el vértice 3 hasta 4 en el grafo con la siguiente matriz de distancias:
Aplicamos el algoritmo de Floyd-Warshall, y para ello en cada iteración fijamos un vértice intermedio.
1ª Iteración: nodo intermedio = 1
La matriz es simétrica, por lo que solamente hará falta calcular el triangulo superior de las distancias.
d23 = min(d23, d21 + d13) = 8
d24 = min(d24, d21 + d14) = 4
d25 = min(d25, d21 + d15) = 9
d26 = min(d26, d21 + d16) = 
d34 = min(d34, d31 + d14) = 6
d35 = min(d35, d31 + d15) = 7
d36 = min(d36, d31 + d16) = 1
d45 = min(d45, d41 + d15) = 
d46 = min(d46, d41 + d16) = 4
d56 = min(d56, d51 + d16) = 
La matriz de distancia después de esta iteración es:
2ª Iteración: nodo intermedio = 2
d13 = min(d13, d12 + d23) = 5
d14 = min(d14, d12 + d24) = 1
d15 = min(d15, d12 + d25) = 12
d16 = min(d16, d12 + d26) = 
d34 = min(d34, d32 + d24) = 6
d35 = min(d35, d32 + d25) = 7
d36 = min(d36, d32 + d26) = 1
d45 = min(d45, d42 + d25) = 13
d46 = min(d46, d42 + d26) = 4
d56 = min(d56, d52 + d26) = 
La matriz de distancia después de esta iteración es:
3ª Iteración: nodo intermedio = 3
d12 = min(d12, d13 + d32) = 3
d14 = min(d14, d13 + d34) = 1
d15 = min(d15, d13 + d35) = 12
d16 = min(d16, d13 + d36) = 6
d24 = min(d24, d23 + d34) = 4
d25 = min(d25, d23 + d35) = 9
d26 = min(d26, d23 + d36) = 9
d45 = min(d45, d43 + d35) = 13
d46 = min(d46, d43 + d36) = 4
d56 = min(d56, d53 + d36) = 8
La matriz de distancia después de esta iteración es:
4ª Iteración: nodo intermedio = 4
d12 = min(d12, d14 + d42) = 3
d13 = min(d13, d14 + d43) = 5
d15 = min(d15, d14 + d45) = 12
d16 = min(d16, d14 + d46) = 5
d23 = min(d23, d24 + d43) = 8
d25 = min(d25, d24 + d45) = 9
d26 = min(d26, d24 + d46) = 8
d35 = min(d35, d34 + d45) = 7
d36 = min(d36, d34 + d46) = 1
d56 = min(d56, d54 + d46) = 8
La matriz de distancia después de esta iteración es:
5ª Iteración: nodo intermedio = 5
d12 = min(d12, d15 + d52) = 3
d13 = min(d13, d15 + d53) = 5
d14 = min(d14, d15 + d54) = 1
d16 = min(d16, d15 + d56) = 5
d23 = min(d23, d25 + d53) = 8
d24 = min(d24, d25 + d54) = 4
d26 = min(d26, d25 + d56) = 8
d34 = min(d34, d35 + d54) = 6
d36 = min(d36, d35 + d56) = 1
d46 = min(d46, d45 + d56) = 4
La matriz de distancia después de esta iteración es:
6ª Iteración: nodo intermedio = 6
d12 = min(d12, d16 + d62) = 3
d13 = min(d13, d16 + d63) = 5
d14 = min(d14, d16 + d64) = 1
d15 = min(d15, d16 + d65) = 12
d23 = min(d23, d26 + d63) = 8
d24 = min(d24, d26 + d64) = 4
d25 = min(d25, d26 + d65) = 9
d34 = min(d34, d36 + d64) = 5
d35 = min(d35, d36 + d65) = 7
d45 = min(d45, d46 + d65) = 12
La matriz de distancia después de esta iteración es:
Ya se han hecho todas las iteraciones posibles. Por tanto, el camino mínimo entre 2 vértices cualesquiera del grafo será el obtenido en la matriz final. En este caso, el camino mínimo entre 3 y 4 vale 5.
7. APLICACIONES
El algoritmo de Floyd-Warshall puede ser utilizado para resolver los siguientes problemas, entre otros:
- Camino mínimo en grafos dirigidos(algoritmo de Floyd).
- Cierre transitivo en grafos dirigidos (algoritmo de Warshall). Es la formulación original del algoritmo de Warshall. El grafo es un grafo no ponderado y representado por una matriz booleana de adyacencia. Entonces la operación de adición es reemplazada por la conjunción lógica(AND) y la operación menor por la disyunción lógica (OR).
- Encontrar una expresión regular dada por un lenguaje regular aceptado por un autómata finito (algoritmo de Kleene).
- Inversión de matrices de números reales(algoritmo de Gauss-Jordan).
- Ruta optima. En esta aplicación es interesante encontrar el camino del flujo máximo entre 2 vértices. Esto significa que en lugar de tomar los mínimos con el pseudocodigo anterior, se coge el máximo. Los pesos de las aristas representan las limitaciones del flujo. Los pesos de los caminos representan cuellos de botella; por ello, la operación de adición anterior es reemplazada por la operación mínimo.
- Comprobar si un grafo no dirigido es bipartito.
BIBLIOGRAFIA.
http://personales.upv.es/arodrigu/grafos/FloydWarshall.htm
http://es.wikipedia.org/wiki/Algoritmo_de_Floyd-Warshall#Ejemplo





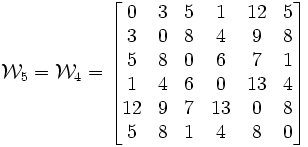

Muy completo.
ResponderEliminar