En ciencias de la computación, el Problema de la cobertura de vértices es un problema NP-completo, que pertenece a los 21 problemas NP-completos de Karp. Es muy utilizado en teoría de complejidad computacional para probar la pertenencia a la clase NP-hard de otros problemas computacionales difíciles.
La cobertura de vértices de un grafo no dirigido G = (V,E) es un subconjunto S de V (el conjunto de vértices) tal que para cada arista ab del conjunto E, ya sea el vértice a o b pertenece a S.
Ejemplo:
En el siguiente grafo
{1,3,5,6} es una cobertura de vértices de tamaño 4. Sin embargo, esta no es la cobertura mínima, porque existen las coberturas de vértices {2,4,5} y {1,2,4}, ambas de tamaño 3. El Problema de cobertura de vértices es un problema de optimización que consiste en encontrar una cobertura de vértices de tamaño k en un grafo dado.
- ENTRADA: Grafo G.
- SALIDA: El menor número k tal que exista una cobertura de vértices S para G de tamaño k.
Equivalentemente, el problema puede definirse como un problema de decisión:
- ENTRADA: Grafo G y un entero positivo k.
- PREGUNTA: ¿Existe una cobertura de vértices S para G de tamaño menor o igual a k?
La cobertura de vértices está estrechamente relacionada con el Problema del conjunto independiente. Un conjunto de vértices S es una cobertura de vértices si y sólo si su complemento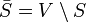 
es un conjunto independiente. Así, un grafo con n vértices tiene una cobertura de vértices de tamaño k si y sólo si el grafo tiene un conjunto independiente de tamaño n-k. En este sentido, cada uno de estos problemas es dual al otro.
NOTA: deje los hipervinculos para mas referencias, maestra si cree que la entrada es muy pobre con gusto explicare este tema en asesorias.
http://es.wikipedia.org/wiki/Problema_de_la_cobertura_de_v%C3%A9rtices
No hay comentarios:
Publicar un comentario