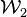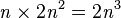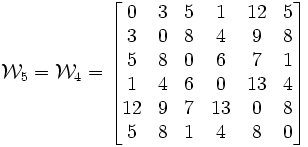Sistemas Numericos (puntos extra)

Un sistema de numeración es un conjunto de símbolos y reglas de generación que permiten construir todos los números válidos en el sistema.

Un sistema de numeración puede representarse como

donde:

• es el sistema de numeración considerado (p.ej. decimal, binario, etc.).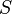
• es el conjunto de símbolos permitidos en el sistema. En el caso del sistema decimal son {0,1,...9}; en el binario son {0,1}; en el octal son {0,1,...7}; en el hexadecimal son {0,1,...9,A,B,C,D,E,F}.
• son las reglas que nos indican qué números son válidos en el sistema, y cuáles no. En un sistema de numeración posicional las reglas son bastante simples, mientras que la numeración romana requiere reglas algo más elaboradas.

Estas reglas son diferentes para cada sistema de numeración considerado, pero una regla común a todos es que para construir números válidos en un sistema de numeración determinado sólo se pueden utilizar los símbolos permitidos en ese sistema.

Para indicar en qué sistema de numeración se representa una cantidad se añade como subíndice a la derecha el número de símbolos que se pueden representar en dicho sistema.

Una tabla de conversion util puede ser esta:

aki se muestran los diferentes valores en los distintos sistemas numericos.

Conversiones

CONVERSIÓN DE UN NUMERO DECIMAL A BINARIO

Para esta transformación es necesario tener en cuenta los pasos que mostraremos en el siguiente ejemplo: Transformemos el numero 42 a numero binario

1. Dividimos el numero 42 entre 2
2. Dividimos el cociente obtenido por 2 y repetimos el mismo procedimiento hasta que el cociente sea 1.
3. El numero binario lo formamos tomando el primer dígito el ultimo cociente, seguidos por los residuos obtenidos en cada división, seleccionándolos de derecha a izquierda, como se muestra en el siguiente esquema.

CONVERSIÓN DE UN NUMERO DECIMAL FRACCIONARIO A UN NUMERO BINARIO

Para transformar un número decimal fraccionario a un numero binario debemos seguir los pasos que mostramos en el siguiente ejemplo: transformemos el numero 42,375.

1. la parte entera se transforma de igual forma que el ejemplo anterior.
2. La parte fraccionaria de la siguiente manera:

• Multiplicamos por el numero 2 y tomamos la parte entera del producto que ira formando el numero binario correspondiente
• Tomamos nuevamente la parte entera del producto, y la parte fraccionaria la multiplicamos sucesivamente por 2 hasta llegar a 0
• Tomamos nuevamente la parte entera , y como la parte fraccionaria es 0, indica que se ha terminado el proceso .El numero binario correspondiente a la parte decimal será la unión de todas las partes enteras, tomadas de las multiplicaciones sucesivas realizadas durante el transcurso del proceso , en donde el primer dígito binario corresponde a la primera parte entera , el segundo dígito a la segunda parte entera , y así sucesivamente hasta llegar al ultimo .Luego tomamos el numero binario , correspondiente a la parte entera , y el numero binario , correspondiente a la parte fraccionaria y lo unimos en un solo numero binario correspondiente a el numero decimal.

CONVERSIÓN DE UN NUMERO BINARIO A UN NUMERO DECIMAL

Para convertir un número binario a decimal, realizamos los siguientes pasos:

1. Tomamos los valores de posición correspondiente a las columnas donde aparezcan únicamente unos
2. Sumamos los valores de posición para identificar el numero decimal equivalente

CONVERSIÓN DE UN NUMERO DECIMAL A OCTAL

Para convertir un numero en el sistema decimal al sistema de numeración Octal, debemos seguir los pasos que mostraremos en el siguiente ejemplo Convertir el numero decimal 323.625 a el sistema de numeración Octal

1. Se toma el numero entero y se divide entre 8 repetidamente hasta que el dividendo sea menor que el divisor, para colocar entonces el numero 0 y pasar el dividendo a formar el primer dígito del numero equivalente en decimal
2. Se toma la parte fraccionaria del numero decimal y la multiplicamos por 8 sucesivamente hasta que el producto no tenga números fraccionarios
3. Pasamos la parte entera del producto a formar el dígito correspondiente
4. Al igual que los demás sistemas , el numero equivalente en el sistema decimal , esta formado por la unión del numero entero equivalente y el numero fraccionario equivalente.

CONVERSIÓN DE UN NUMERO OCTAL A BINARIO

La ventaja principal del sistema de numeración Octal es la facilidad conque pueden realizarse la conversión entre un numero binario y octal. A continuación mostraremos un ejercicio que ilustrará la teoría. Por medio de este tipo de conversiones, cualquier numero Octal se convierte a binario de manera individual. En este ejemplo, mostramos claramente el equivalente 100 111 010 en binario de cada numero octal de forma individual.

CONVERSIÓN DE UN NUMERO DECIMAL A UN NUMERO HEXADECIMAL

Convertir el numero 250.25 a Hexadecimal

1. Se toma la parte entera y se divide sucesivamente por el numero decimal 16 (base) hasta que el cociente sea 0
2. Los números enteros resultantes de los cocientes, pasarán a conformar el numero hexadecimal correspondiente, teniendo en cuenta que el sistema de numeración hexadecimal posee solo 16 símbolos, donde los números del 10 hasta el 15 tienen símbolos alfabéticos que ya hemos explicado
3. La parte fraccionaria del numero a convertir se multiplica por 16 (Base) sucesivamente hasta que el producto resultante no tenga parte fraccionaria
4. Al igual que en los sistemas anteriores, el numero equivalente se forma, de la unión de los dos números equivalentes, tanto entero como fraccionario, separados por un punto que establece la diferencia entre ellos.

CONVERSIÓN DE UN NUMERO HEXADECIMAL A UN NUMERO DECIMAL

Como en los ejemplos anteriores este también nos ayudará a entender mejor este procedimiento: Convertir el numero hexadecimal 2B6 a su equivalente decimal.

1. Multiplicamos el valor de posición de cada columna por el dígito hexadecimal correspondiente.
2. El resultado del número decimal equivalente se obtiene, sumando todos los productos obtenidos en el paso anterior.

Fuentes:

http://ladelec.com/teoria/electronica-digital/148-conversiones-de-sistemas-de-numeracion.html

http://es.wikipedia.org/wiki/Sistema_de_numeraci%C3%B3n#Tabla_de_conversi.C3.B3n_entre_decimal.2C_binario.2C_hexadecimal.2C_octal.2C_BCD.2C_Exceso_3_y_Gray_o_Reflejado

Cobertura de vertices (puntos extra)

Tema del proyecto 5 no estoy muy seguro si alguien lo explico en clase pero aqui se los pongo en mi blog Cobertura de vertices.

En ciencias de la computación, el Problema de la cobertura de vértices es un problema NP-completo, que pertenece a los 21 problemas NP-completos de Karp. Es muy utilizado en teoría de complejidad computacional para probar la pertenencia a la clase NP-hard de otros problemas computacionales difíciles.

La cobertura de vértices de un grafo no dirigido G = (V,E) es un subconjunto S de V (el conjunto de vértices) tal que para cada arista ab del conjunto E, ya sea el vértice a o b pertenece a S.

Ejemplo:

En el siguiente grafo

{1,3,5,6} es una cobertura de vértices de tamaño 4. Sin embargo, esta no es la cobertura mínima, porque existen las coberturas de vértices {2,4,5} y {1,2,4}, ambas de tamaño 3.

El Problema de cobertura de vértices es un problema de optimización que consiste en encontrar una cobertura de vértices de tamaño k en un grafo dado.

ENTRADA: Grafo G.

SALIDA: El menor número k tal que exista una cobertura de vértices S para G de tamaño k.

Equivalentemente, el problema puede definirse como un problema de decisión:

ENTRADA: Grafo G y un entero positivo k.

PREGUNTA: ¿Existe una cobertura de vértices S para G de tamaño menor o igual a k?

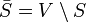La cobertura de vértices está estrechamente relacionada con el Problema del conjunto independiente. Un conjunto de vértices S es una cobertura de vértices si y sólo si su complemento es un conjunto independiente. Así, un grafo con n vértices tiene una cobertura de vértices de tamaño k si y sólo si el grafo tiene un conjunto independiente de tamaño n-k. En este sentido, cada uno de estos problemas es dual al otro.

NOTA: deje los hipervinculos para mas referencias, maestra si cree que la entrada es muy pobre con gusto explicare este tema en asesorias.

http://es.wikipedia.org/wiki/Problema_de_la_cobertura_de_v%C3%A9rtices

RESPUESTA AL EXAMEN "GRAFOS" (puntos extra)

Hola buenas tarde mi nombre es Gustavo adolfo salas coronado y esta es una respuesta al examen ordinario que es del problema de grafos.

·Demuestre que el grafo simple no dirigido definido por las siguientes aristas en formato (inicial, final) es plano: (1,2), (1,3), (1,4), (2,4),(2,6),(3,5), (3,6), (4,5) (5,6).

El grafo es plano ya que ninguno de sus vertices se intersectan.

Diametro: 2
Grado: 3
impresion : 6,5,4,2,1,3

PROYECTO #5

Algoritmo de Floyd-Warshall.

Hola a todos mi nombre es Gustavo Adolfo Salas Coronado de la clase de los jueves de v1 a v3 y este es mi proyecto y explicare cada uno de los puntos requeridos:

1- Problema que este algoritmo resuelve.

El algoritmo de Floyd-Warshall, descrito en 1959 por Bernard Roy, es un algoritmo de análisis sobre grafos para encontrar el camino minimo en grafos dirigidos ponderados. El algoritmo encuentra el camino entre todos los pares de vértices en una única ejecución. El algoritmo de Floyd-Warshall es un ejemplo de programacion dinamica.

2.- Definicion formal.

Pues el algoritmo de Floyd-Warshall compara todos los posibles caminos a través del grafo entre cada par de vértices. El algoritmo es capaz de hacer esto con sólo V³ comparaciones (esto es notable considerando que puede haber hasta V² aristas en el grafo, y que cada combinación de aristas se prueba). Lo hace mejorando paulatinamente una estimación del camino más corto entre dos vértices, hasta que se sabe que la estimación es óptima, por lo tanto es un algoritmo de OPTIMIZACION.

3.-La complejidad computacional de este algoritmo es de tipo P determinista ya que puede ser resuelto por una maquina turing determinista en tiempo polinomico.

4.-Pseudocodigo.

Inicializar
D = A ' matriz de distancias = matriz de arcos

si i=j o Dij= infinito entonces Pi,j = nulo sino Pi,j=i 'matriz de caminos

for k = 1 to V
for i = 1 to V
for j = 1 to V
Di,j = min(Di,j , Di,k + Dk,j )
si min = Di,k + Dk,j entonces
Pi,j = Pk,j
fin

5.- Analisis asintotico.

Si utilizamos matrices booleanas, para encontrar todos los n² de desde se necesita hacer 2n² operaciones binarias. Debido a que empezamos con y computamos la secuencia de n matrices booleanas , , ..., , el número total de operaciones binarias es de . Por lo tanto, la complejidad del algoritmo es Θ(n³) y puede ser resuelto por una maquina determinista de turing en tiempo polinomico.

6.- EJEMPLO.

Hallar el camino mínimo desde el vértice 3 hasta 4 en el grafo con la siguiente matriz de distancias:

Aplicamos el algoritmo de Floyd-Warshall, y para ello en cada iteración fijamos un vértice intermedio.

1ª Iteración: nodo intermedio = 1

La matriz es simétrica, por lo que solamente hará falta calcular el triangulo superior de las distancias.

d₂₃ = min(d₂₃, d₂₁ + d₁₃) = 8

d₂₄ = min(d₂₄, d₂₁ + d₁₄) = 4

d₂₅ = min(d₂₅, d₂₁ + d₁₅) = 9

d₂₆ = min(d₂₆, d₂₁ + d₁₆) =

d₃₄ = min(d₃₄, d₃₁ + d₁₄) = 6

d₃₅ = min(d₃₅, d₃₁ + d₁₅) = 7

d₃₆ = min(d₃₆, d₃₁ + d₁₆) = 1

d₄₅ = min(d₄₅, d₄₁ + d₁₅) =

d₄₆ = min(d₄₆, d₄₁ + d₁₆) = 4

d₅₆ = min(d₅₆, d₅₁ + d₁₆) =

La matriz de distancia después de esta iteración es:

2ª Iteración: nodo intermedio = 2

d₁₃ = min(d₁₃, d₁₂ + d₂₃) = 5

d₁₄ = min(d₁₄, d₁₂ + d₂₄) = 1

d₁₅ = min(d₁₅, d₁₂ + d₂₅) = 12

d₁₆ = min(d₁₆, d₁₂ + d₂₆) =

d₃₄ = min(d₃₄, d₃₂ + d₂₄) = 6

d₃₅ = min(d₃₅, d₃₂ + d₂₅) = 7

d₃₆ = min(d₃₆, d₃₂ + d₂₆) = 1

d₄₅ = min(d₄₅, d₄₂ + d₂₅) = 13

d₄₆ = min(d₄₆, d₄₂ + d₂₆) = 4

d₅₆ = min(d₅₆, d₅₂ + d₂₆) =

La matriz de distancia después de esta iteración es:

3ª Iteración: nodo intermedio = 3

d₁₂ = min(d₁₂, d₁₃ + d₃₂) = 3

d₁₄ = min(d₁₄, d₁₃ + d₃₄) = 1

d₁₅ = min(d₁₅, d₁₃ + d₃₅) = 12

d₁₆ = min(d₁₆, d₁₃ + d₃₆) = 6

d₂₄ = min(d₂₄, d₂₃ + d₃₄) = 4

d₂₅ = min(d₂₅, d₂₃ + d₃₅) = 9

d₂₆ = min(d₂₆, d₂₃ + d₃₆) = 9

d₄₅ = min(d₄₅, d₄₃ + d₃₅) = 13

d₄₆ = min(d₄₆, d₄₃ + d₃₆) = 4

d₅₆ = min(d₅₆, d₅₃ + d₃₆) = 8

La matriz de distancia después de esta iteración es:

4ª Iteración: nodo intermedio = 4

d₁₂ = min(d₁₂, d₁₄ + d₄₂) = 3

d₁₃ = min(d₁₃, d₁₄ + d₄₃) = 5

d₁₅ = min(d₁₅, d₁₄ + d₄₅) = 12

d₁₆ = min(d₁₆, d₁₄ + d₄₆) = 5

d₂₃ = min(d₂₃, d₂₄ + d₄₃) = 8

d₂₅ = min(d₂₅, d₂₄ + d₄₅) = 9

d₂₆ = min(d₂₆, d₂₄ + d₄₆) = 8

d₃₅ = min(d₃₅, d₃₄ + d₄₅) = 7

d₃₆ = min(d₃₆, d₃₄ + d₄₆) = 1

d₅₆ = min(d₅₆, d₅₄ + d₄₆) = 8

La matriz de distancia después de esta iteración es:

5ª Iteración: nodo intermedio = 5

d₁₂ = min(d₁₂, d₁₅ + d₅₂) = 3

d₁₃ = min(d₁₃, d₁₅ + d₅₃) = 5

d₁₄ = min(d₁₄, d₁₅ + d₅₄) = 1

d₁₆ = min(d₁₆, d₁₅ + d₅₆) = 5

d₂₃ = min(d₂₃, d₂₅ + d₅₃) = 8

d₂₄ = min(d₂₄, d₂₅ + d₅₄) = 4

d₂₆ = min(d₂₆, d₂₅ + d₅₆) = 8

d₃₄ = min(d₃₄, d₃₅ + d₅₄) = 6

d₃₆ = min(d₃₆, d₃₅ + d₅₆) = 1

d₄₆ = min(d₄₆, d₄₅ + d₅₆) = 4

La matriz de distancia después de esta iteración es:

6ª Iteración: nodo intermedio = 6

d₁₂ = min(d₁₂, d₁₆ + d₆₂) = 3

d₁₃ = min(d₁₃, d₁₆ + d₆₃) = 5

d₁₄ = min(d₁₄, d₁₆ + d₆₄) = 1

d₁₅ = min(d₁₅, d₁₆ + d₆₅) = 12

d₂₃ = min(d₂₃, d₂₆ + d₆₃) = 8

d₂₄ = min(d₂₄, d₂₆ + d₆₄) = 4

d₂₅ = min(d₂₅, d₂₆ + d₆₅) = 9

d₃₄ = min(d₃₄, d₃₆ + d₆₄) = 5

d₃₅ = min(d₃₅, d₃₆ + d₆₅) = 7

d₄₅ = min(d₄₅, d₄₆ + d₆₅) = 12

La matriz de distancia después de esta iteración es:

Ya se han hecho todas las iteraciones posibles. Por tanto, el camino mínimo entre 2 vértices cualesquiera del grafo será el obtenido en la matriz final. En este caso, el camino mínimo entre 3 y 4 vale 5.

7. APLICACIONES

El algoritmo de Floyd-Warshall puede ser utilizado para resolver los siguientes problemas, entre otros:

• Camino mínimo en grafos dirigidos(algoritmo de Floyd).
• Cierre transitivo en grafos dirigidos (algoritmo de Warshall). Es la formulación original del algoritmo de Warshall. El grafo es un grafo no ponderado y representado por una matriz booleana de adyacencia. Entonces la operación de adición es reemplazada por la conjunción lógica(AND) y la operación menor por la disyunción lógica (OR).
• Encontrar una expresión regular dada por un lenguaje regular aceptado por un autómata finito (algoritmo de Kleene).
• Inversión de matrices de números reales(algoritmo de Gauss-Jordan).
• Ruta optima. En esta aplicación es interesante encontrar el camino del flujo máximo entre 2 vértices. Esto significa que en lugar de tomar los mínimos con el pseudocodigo anterior, se coge el máximo. Los pesos de las aristas representan las limitaciones del flujo. Los pesos de los caminos representan cuellos de botella; por ello, la operación de adición anterior es reemplazada por la operación mínimo.
• Comprobar si un grafo no dirigido es bipartito.

BIBLIOGRAFIA.

http://personales.upv.es/arodrigu/grafos/FloydWarshall.htm
http://es.wikipedia.org/wiki/Algoritmo_de_Floyd-Warshall#Ejemplo

PROYECTO #4 "Listas Simplemente Enlazadas"

Hola mi nombre es Gustavo Adolfo Salas Coronado y me toco el tema de Listas Simplemente Enlazadas, trabajo que terminamos a tiempo con la ayuda de mis compañeros que son:

http://raulelchupete.blogspot.com/
http://hiram-algoritmos.blogspot.com/
http://www.eddypre.blogspot.com/


¿En que contribui en el trabajo?

La parte que me toco a mi fue definir lo que es una lista simplemente enlazadas, fue algo facil ya que muchos sitios web muestran ejemplos claros del tema, busque las definiciones y las mande a mis compañeros para que las agregaran a las diapositivas.


¿En que aspectos estoy bien y en cuales necesito mejorar?

Me parece que la tarea que se me encomendo la realize bien, soy bueno buscando informacion ya que siempre me pongo a leer lo que estoy buscando y las diferentes opciones, la mas coherente es la que elijo, un aspecto que me gustaria mejorar seria la comprension de la informacion que estoy buscando ya que algunas veces no comprendo bien o tardo algo de tiempo en hacerlo.

¿Ayudo a los demas o me apoyo en ellos?

Si, nos ayudamos mutuamente entre nosotros son las ventajas de trabajar en equipo el poder apoyarte en los demas y cuando alguien lo requiera tambien la informacion que tienes puede ser de utilidad.

¿Que papel tome yo en el trabajo?

Insisto que cada quien toma un papel igualmente importante que el de tu compañero ya que en un equipo siempre hay que estar unidos, mi papel fue el de reunir la informacion acerca de las listas y en la clase me tocara exponer lo que es la introduccion al tema.

Reflexion personal.

Trabajar en equipo es mejor, ya que la carga de trabajo es menor y tienes a alguien en quien apoyarte. Con mi equipo trabajo de forma adecuada y siempre cumpliendo.

Estas son las diapositivas al trabajo:

Lse(jueves)

View more presentations from guest046242.

PROYECTO 3 "MAXIMO COMUN DIVISOR"

Hola, mi nombre es Gustavo Adolfo Salas Coronado pertenezco al grupo de los jueves y este es mi proyecto numero 3 que hize con mis compañeros de equipo

Carlos Triana Sarmiento http://www.eddypre.blogspot.com
Hiram Martinez Torres http://hiramalgoritmos.blogspot.com/
Fernando Aguilar http://algoritmosfernando.blogspot.com/




1.-Un algoritmo recursivo se usa cuando un programa que es corto necesita repetir ciertos ciclos para ello tambien se simplifica la escritura del pseudocodigo, haciendolo mas largo pero mas facil de analizar y entender. Cuando se usa un algoritmo recursivo se consumen mas recursos del sistema como memoria o uso del procesador, si se tiene una buena memoria y un buen procesador es recomendable usar algoritmos recursivos, pero si no se cuenta con tales recursos pues lo mas conveniente seria usar un algoritmo iterativo.

el siguiente es un ejemplo de un algoritmo recursivo que es el que viene en nuestra presentacion:

00.INICIO
01 .int a, b, p, q, r, mcd //Declaración de variables todas enteras
02 .IMPRESION (Introduzca dos números enteros y positivos)
//Introducción de los numero enteros
03. DATOS(a, b) //Datos en este ejemplo yo puse un 32 y un 56
04 .WHILE( a <= 0 || b <= 0 ) //Esta condición no se cumple porque no introduje
//números negativos, esta condición es solo para evitar los números negativos
05 .IMPRESION(Los números deben ser positivos, Introduzca nuevamente)
//Impresión de arriba en caso de introducir números negativos
06 .DATOS(a, b) //Datos en este ejemplo yo puse un 32 y un 56
07 .IF(a < b) //La condición se cumple porque 32<56
//Por lo tanto se ejecuta el código siguiente:
08 .p = b //Estas igualdades de variables solo son para
09 .q = a //representar el orden de los números en las operaciones
//En este caso p=56 y q=32
10 .ELSE
11 .p = a //Si no se cumpliera la condición pasada(a
12 .q = b //Este seria el orden que llevaría la operación
13 .r = p%q //Por lo tanto r=56%32, r=24
14 .WHILE ( r != 0 ) //Vemos que r=24 y cumple la condición(r!=0)
//Por lo y tanto se ejecuta todo el siguiente código donde se igualan las variables iniciales a otras
nuevas, para que se cumpla la secuencia de Máximo común divisor
15 .p = q //En este caso p=32
16 .q = r //Recordemos el valor de r=24, por lo tanto q=24
17.r = p%q //Ahora calculamos un nuevo valor de r
//r=32%24 r=8, y la condición de while es (r!=0) entonces se sigue ejecutando el código.
//Ahora p=q, q=r, p=24,q=8
//Seguimos con la operación r=p%q, r=24%8, r=0
//Con esto se rompe el ciclo while(r!=0) porque r=0
//Se sale del ciclo y continua con las siguientes lineas de código
18.mcd= q
//Recordando que nuestra ultima q=8, mcd =8
19.IMPRESION( a, b, mcd) //Impresión los 2 valores ingresados y su mcd.
20.FIN


2.-Bueno la verdad siempre la ventaja de trabajar como grupo es que siempre hay un margen mas amplio de ideas que aportar, con ello se logra realizar un trabajo muy bien hecho. Las ideas que aporta cada integrante son de vital importancia se toman en cuenta todas las ideas y se unen para formar una sola que seria la que termine plasmada en el trabajo.

3.-Mi contribucion al trabajo fue lo del ultimo punto que fue lo de:

Conclusiones y recomendaciones sobre cuándo usar
recursión y cuándo iteración.

4.-La verdad yo pienso que cada kien hizo muy bien su parte, ya que si alguien faltar tendriamos un trabajo incompleto y pues lo que me toco a mi es de la misma importancia que lo que le toco hacer a los demas del ekipo.

5.-En un futuro se podria mejorar estudiando mas sobre el tema y metiendose mas a fondo, con esto me imagino q los trabajos serian de mayor calidad y mas faciles de hacer.

LAS LIGAS A LOS BLOGS YA LAS PUSE ARRIBA.


ENTONCES PUES ESTA ES LA LIGA A LAS DIAPOSITIVAS ESTA ALOJADA EN MEGAUPLOAD.

http://www.megaupload.com/?d=D2SS5NNS


bueno eso es todo gracias por la atencion.

PROYECTO #2

Hola mi nombre es Gustavo Adolfo Salas Coronado estoy en la clase de los jueves de v1-v3 y esta es mi investigacion.



Codigos de Huffman

Los códigos de Huffman son una técnica muy útil para comprimir ficheros.
El algoritmo voraz de Huffman utiliza una tabla de frecuencias de aparición de cada carácter para construir una forma óptima de representar los caracteres con códigos binarios.

Ejemplos:

Se tiene un fichero con 100.000 caracteres que se desea compactar. Las frecuencias de aparición de caracteres en el fichero son las siguientes:


Puede usarse un código de longitud fija (de 3 bits). El fichero requeriría 300.000 bits.


Puede hacerse mejor con un código de longitud variable, dando codificaciones cortas a los caracteres más frecuentes y más largas a los menos frecuentes.Este código ahorra algo más del 25% (requiere 224.000 bits en lugar de 300.000).


Se precisa un código libre de prefijos:
–Ninguna codificación puede ser prefijo de otra.
–De esta forma, la decodificación es inmediata pues no hay ambigüedades.
–Por ejemplo: „001011101‟ sólo puede ser „aabe‟.

El código se representa mediante un trie(árbol lexicográfico):
–árbol binario cuyas hojas son los caracteres codificados;
–el código de cada carácter es el camino desde la raíz hasta la hoja, donde ir al hijo izquierdo significa 0 e ir hacia el derecho significa 1.

Ejemplo: árboles de los dos códigos anteriores.



–Cada hoja está etiquetada con un carácter y su frecuencia.
–Cada nodo interno está etiquetado con la suma de los pesos de las hojas de su subárbol.
–Un código óptimo siempre está representado por un árbol lleno:cada nodo interno tiene dos hijos.
Si el alfabeto que se quiere codificar es C, entonces el árbol del código óptimo tiene |C| hojas y |C|-1 nodos internos.

• El algoritmo voraz de Huffman construye el árbol Ade un código óptimo de abajo hacia arriba.
• Utiliza una cola Q de árboles con prioridades (las frecuencias hacen de prioridades).
• Empieza con un conjunto de |C| hojas en Q y realiza una secuencia de |C|-1 “mezclas” hasta crear el árbol final.
• En cada paso, se “mezclan” los dos objetos (árboles) de Q que tienen menos frecuencia y el resultado es un nuevo objeto (árbol) cuya frecuencia es la suma de las frecuencias de los dos objetos mezclados.

Y aqui el algoritmo:

Inicio
{Pre: C es el conjunto de caracteres y f es el
vector de frecuencias}
funciónHuffman(C:conjunto;f:vectFrec)
devuelveárbol
variablesQ:colaPri; i,fx,fy,fz:entero;
z,x,y:árbol
principio
creaVacía(Q);
para todox en C hacer
inserta(Q,)
fpara;
parai:=1 hasta|C|-1 hacer
:=primero(Q); borra(Q);
:=primero(Q); borra(Q);
fz:=fx+fy;
z:=creaÁrbol(raíz=>fz,
hijoIzq=>x;
hijoDer=>y);
inserta(Q,)
fpara;
:=primero(Q); borra(Q)
devuelvez
fin
{nota: z es el árbol de un código libre de
prefijos óptimo para (C,f)}

Para el ejemplo anterior esta lo siguiente:




Esto es un problema np ya que muestra diferentes soluciones.


Bueno pues eso es todo mi investigacion la sake de un archivo pdf que lo podran encontrar en el siguiente link http://www.slideshare.net/mejiaff/varios-algoritmos-voraces-de-decisin-y-optimizacin.

Me despido gracias por visitar mi blog

Proyecto I

PROYECTO I.

hola mi nombre es Gustavo Salas y el nombre de mi compañera es Ana valeria Aguayo su blog lo pueden encontrar en el sig link http://alcompvaleriardz.blogspot.com/. Lo siguiento es lo proyecto que realizamos.


El problema es:



Colocar un grupo de libros en un librero en orden alfabético según el título.Lo primero que hicimos es crear nuestro algoritmo que es el siguiente:


1. Inicio


2.Tomar un libro


3.Checar la letra inicial del título


4.Revisar en el librero los demás libros

5.Acomodar el libro correctamente

6.Hacer lo mismo con los otros libros que se desean acomodar

7.Fin




De este algoritmo se deriva el siguiente diagrama de flujo

si no alcanzan a apreciar bien la imagen este es el link:

http://i690.photobucket.com/albums/vv263/ant34i/diagrama.jpg

Lo que hace este diagrama es:

1.- Tomar el libro que se desea acomodar
2.-Revisa la letra incial del titulo del libro
3.-Ahora lo que hace es revisar que otros libros no tengan la misma letra inicial.

• En caso de que la primera letra coincida con la de otro libro, se revisa la segunda letra del titulo y si siguen coincidiendo se revisa la tercera letra y asi conscutivamente hasta que las letras no coincidan.
• En el otro caso que seria que las letras no coincidieran se acomoda el libro en su lugar.

4.-Finalmente si aun hay libros que se necesiten acomodar se vuelve a repetir el mismo ciclo en caso de que ya no queden mas libros el proceso llega a su fin.

Esto es todo por mi parte espero y mi trabajo les sea de su agrado y me despido.

MUCHAS GRACIAS POR VISITAR MI BLOG.